1 Storage fault-tolerant coding evaluation index
In the past 20 years, with the rapid development of computer technology, the development of large-scale storage systems has also been very rapid. At present, the memory capacity of ordinary PCs has reached the terabit level, which is 10,000 times higher than the 20 MB storage capacity 20 years ago.
In addition to traditional disk drives, new types of solid-state storage (SSD) memory have also entered the market. Despite the rapid development of the capacity of a single memory, it still can not keep up with the growth rate of people's demand for storage capacity.
With the transformation of large computer systems from "computing as the center" to "information processing as the center", and the explosive growth of the amount of information, people's demand for mass storage systems is increasing. The mass storage system is essentially a lot of single storage devices (the disks are taken as examples in the following) through the interface of the system, connected and integrated into a virtual single storage with huge capacity, that is, disk array.
As the number of disks in the array increases, the reliability of the system also decreases. The industry generally uses MTTDL to measure the reliability of arrays.
If the average failure time of a single disk is MTTFdisk, for a non-redundant array containing n disks, the MTTDL can be simply estimated as: MTTDL = MTTFdisk / n It can be seen that when n is larger, the reliability of the entire system will decrease in proportion. This is unacceptable for larger scale systems. Using redundant data coding to improve system reliability is a well-recognized method to solve this problem. By cleverly adding data on m blocks of standard-size disks, adding part of the redundancy check information, and storing them on n disks after encoding, the system is satisfied: for any k-disk failure, all other nk blocks can be passed When the data in the disk is decoded and restored, the entire system is said to be k fault-tolerant, or k is the fault-tolerant number of the system.
The analysis shows that [1], for a k-tolerant system, it can be approximated as:
Therefore, in large-scale systems, fault tolerance can be said to be another way to describe the reliability of the system. The MTTFdisk of a general disk in the market is around 105, and the system repair time MTTR is generally around 10. According to formula (1), it can be seen that when the number of system disks is 103 to 104, generally, 2 fault tolerance or 3 fault tolerance coding can basically meet the fault tolerance requirements of the storage system.
The more redundancy the system adds to increase fault tolerance, the higher the additional cost of the system. Therefore, under the premise of having the same number of fault tolerances, people often pursue a smaller redundancy, that is, the value of (nm) / n, where n is the number of system disks and m is the number of disks storing user data. According to the Singleton bound of coding theory, the minimum redundancy of k fault-tolerant systems is: k / n. The encoding method that reaches this minimum value is called the MDS code. Most of the current research on memory coding focuses on constructing MDS codes with different parameters.
In addition to the above indicators, the speed and efficiency of any computer system are always important indicators to be considered. Here we do not discuss how to effectively process data reads from multiple disks in parallel (that is another large issue), but focus on the extra computational overhead due to redundant encoding. For even the same encoding method, due to different encoding / decoding algorithms, there may be a large difference in calculation efficiency. In a computer system, the final encoding operation will be reflected as some binary operations, so researchers usually use the total number of binary XOR operations required by the encoding to measure the system computing overhead due to additional redundant encoding. For a random access storage system, the performance of random small block information write operations is particularly important. The average XOR times that each unit participates in the encoding operation can be used to measure this indicator, which we call the update complexity of the encoding.
Based on the above discussion, the fault-tolerant coding problem of the storage system can be attributed to the search for coding methods that optimize the following indicators
The system satisfies the required fault tolerance performance, and the fault tolerance number is k.
The system has a small (or optimal) redundancy
The system has a small (or optimal) coding / update complexity.
2 Linear coding
For a single fault-tolerant system, a simple parity check can make the above three indicators optimal. Classical systems use this method. However, for the case where k is greater than 1, the solution to the problem is not so simple. From the rich results of communication coding theory, two more representative coding methods were selected by people and used to solve the problem of storage fault tolerance. They are binary linear codes and RS codes.
2.1 Multi-dimensional array code
Figure 1 shows the two-dimensional array coding and parity check matrix. The two-dimensional array code is a natural extension of parity check. It is easy to see from Figure 1 that it is double fault-tolerant. The two-dimensional array code maintains the characteristic of the optimal coding complexity of the parity check code in single fault tolerance, but the redundancy of the two-dimensional array code is no longer optimal.
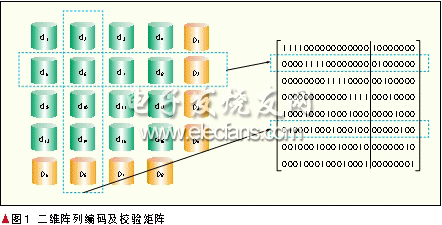
Two-dimensional array codes can also be easily extended to k-dimensional arrays. And it is easy to obtain the k-tolerant characteristic of such encoding. However, as k increases, the redundancy will become larger and larger [2-3].
2.2 Full code
Figure 2 shows the FULL-2 code. FULL-2 codes can be regarded as the promotion of two-dimensional array codes.

The FULL code still maintains the optimal coding complexity, and the redundancy is much better than the array code. Unfortunately, when k is greater than 3, FULL-k codes are no longer k-tolerant [4].
Fiber Optic Box,Fiber Optics Box,Fiber Optic Boxes,Fiber Optic Junction Box
Cixi Dani Plastic Products Co.,Ltd , https://www.cxdnplastic.com